Headline: Chinese Researchers Use Quantum Computer to Defeat RSA! Encryption is DEAD!

Article: They used a quantum computer to crack a 50 bit RSA key.

Current recommended key length for RSA? 2048 bits.

So I think we're safe, for now.

@mainframed767 It's only a matter of time!!!11111

Everyone buy my post-quantum-safe crypto gadget.

Wait, no, that's wrong.

Everybody RENT my post-quantum-safe crypto SaaS gadget!

@christopherkunz Please sign up to my post Quantum-AGI safe crypto scheme, licensed per seat. No you can't see the source.

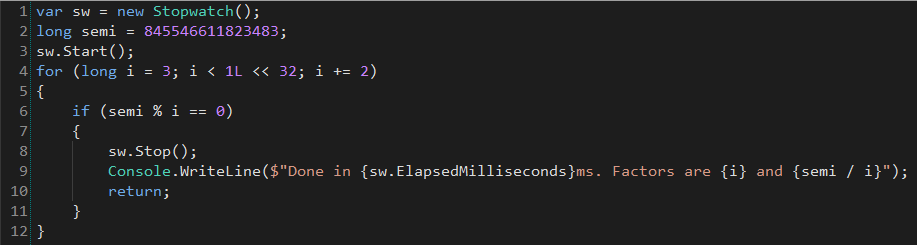
@mainframed767 I took the 50-bit semiprime from their paper and factorised it on a 2.2GHz x86_64 CPU core (Xeon 8276L, so not optimised for single core workloads at all) using the most naive brute force factoring implementation there is, and it took 95ms.

I'm not exactly worried here.

@gsuberland now try that with 2048.

Scaling up this experiment will result in the same time for 50 bits as 2048.

@mainframed767

@bobdobberson @mainframed767 that's not really an accurate representation of the problem though. Shor's algorithm is O(log N) so the semiprime factorisation time is pretty small, but the gate count required is a completely different story, scaling in excess of the log squared. for 2048-bit the most gate-conservative approach requires roughly ~1M times as many gates as the largest QCs we have today, and requires solving decoherence at that scale. we don't know how to do that.

@bobdobberson @mainframed767 I'm sure eventually we'll figure out a way to do it, but that will be on a timescale far exceeding our ability to migrate to PQC algorithms, rendering it largely moot except for captured historical data.

@gsuberland if the experiment is scaled to factor 2048 bit keys that's a hardware issue, correct?

With the hardware, the timing would be the same as (or faster, with improvements) the 50 bit experiment we're reading about. Right?

@mainframed767

@bobdobberson @mainframed767 it's O(log N) so about 600 times slower, but yes.

"just scale the hardware" is not something we can just do. there are fundamental physics problems and limits we hit when trying to do so, which is why QCs have such tiny gate counts so far. the complexity scales nonlinearly, so doubling the gate count is a huge undertaking.

@gsuberland don't forget about the exabytes of 2048 bit encrypted data that intelligence agencies are waiting patiently to open up.

@mainframed767

@bobdobberson @mainframed767 that's what I just said, yes.

@gsuberland how does big O relate to quantum where we're talking about the collapse of superpositions?

@mainframed767

@bobdobberson @mainframed767 I suggest the Wikipedia page for Shor's algorithm as a good place to start if you want to understand that.

@gsuberland your points are taken. I personally find this exciting because from what I can tell, it's the first PoC of something that's been talked about for decades.

@mainframed767

@bobdobberson @mainframed767 it's not, we've done factorisation tons of times on QCs. it was literally the hello world demo that D-wave did way back when they first debuted.

@gsuberland it can be difficult to learn about quantum without having good advisors on the subject, given the level of hype associated with it.

Can you link to some of the earliest experiments proving Shor's algorithm can work with quantum to break low bit RSA keys?

@mainframed767

@bobdobberson @mainframed767 I don't really have time to dig through the literature for you. Searching for semiprime factorisation instead of "breaks RSA" or whatever should get you better results on your searches since that's what is happening here.

@gsuberland looks like it was published as early as 2012 for N=21, which I presume is 21 bits, but I'm out of my depth.

http://qcmc2012.org/wp-content/uploads/2012/08/Poster_Martin-Lopez.pdf

@mainframed767

@bobdobberson @mainframed767 N=21 means they factored 21 into 7 and 3. that would've been the first, most likely, since 3 is the smallest prime of note in this context.

the N is the actual number, not the size of the number, so for a 2048-bit semiprime N is 2^2048 (about 3.2*10^616)

@gsuberland so 5 bits 12 years ago, 50 bits today, 500 bits in 6 more years?

@mainframed767

@bobdobberson @mainframed767 you can't really linearly extrapolate because the problem isn't as simple as just making a bigger system. there are a ton of externalities involved and you can't really measure it like we do Moore's law (for the time that it remained valid, at least). some of it will happen incrementally, but a lot of it is more like trying to predict when we'll solve unsolved problems in physics and maths.

@bobdobberson @mainframed767 it's definitely nothing like the "more cores, faster GPUs, faster memory, bigger storage, faster network" progression we see in classical computing. it's really better to think of them less like computers and more like a particle collider in terms of the problem domain.

@gsuberland oh, I know, I'm just spitballing. I presume it's going to be closer to 2 years.

@mainframed767

@bobdobberson @mainframed767 no, definitely not. you'd be closer if you said 20.

@gsuberland that's a good way of putting it, and one of the reasons quantum has been difficult for me to find anything fascinating enough about to learn and play around with.

I know there are some simulators we can access to get an idea of how to throw problems at it, but it's a domain very few of us have an ability for hands-on.

As soon as I realized you don't run a shell or OS on a quantum computer, it became a peripheral in my mind.

In this case, my mind believes it's just a matter of having a peripheral with enough qubits to tackle the numbers that need to be processed -- like going from 32 bit to 64 bit registers.

So it seems probable to me that if they can handle a 50 bit number and the decoherence/noise to make it useful, it's simply a matter of scaling up that register.

Maybe it takes 4x the qubits to go from 50 to 51 bits, but eventually, someone will build a large enough register to hold the data that needs to be factored / worked on.

@mainframed767

@bobdobberson @mainframed767 you're still thinking of this too linearly. qubits aren't like bits in a register, you can't just add more like you're sticking lego bricks together or widening an FPGA register. it's not like "oh we just shove more power in". the more you add, the harder it gets to add more, with combinatorial effect. "simply a matter of scaling up" skips over this enormous problem space that gets harder the further you try to push it. we don't even know if we can achieve it yet.

@gsuberland @mainframed767 it's an advancement on the problem. That's it. Everything else was sensationalism from media. Every advancement on factorization is a reason to review how quickly PQC gets rolled out so it is in widespread use before real attacks are possible.

@mxshift @mainframed767 yup, exactly.